
Open menu
Si vuole ricavare la formula risolutiva dell'equazione di secondo grado completa.
In primo luogo si trasporta il termine noto c al secondo membro
ax2+bx=-c
Si moltiplica per 4a entrambi i membri, ottenendo:
4a2x2+4abx=-4ac
Si osservi che 4a2x2=(2ax)2 e 4abx =2·(2ax)·b
cioè al primo membro il primo termine è il quadrato di un monomio, mentre il secondo termine è il doppio prodotto di 2ax e b
si aggiunge b2 al primo ed al secondo membro in modo da avere al primo membro il quadrato del binomio 2ax+b.
4a2x2+4abx+b2=b2-4ac cioè (2ax+b)2=b2-4ac.
Estraendo la radice quadrata ad ambo i membri si ottiene
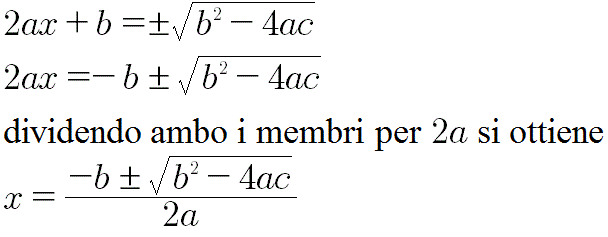
Affinchè le soluzioni siano reali occorre che il radicando non sia negativo.
Questo radicando b2-4ac si chiama discriminante dell'equazione di secondo grado e si indica con la lettera Δ
A seconda del valore di Δ si possono presentare tre casi:
In determinate situazioni è possibile trovare le soluzioni senza applicare la formula risolutiva.
Dalla formula risolutiva si deducono le seguenti relazioni:
In particolare quando a=1 e le soluzioni sono numeri interi, per trovare le soluzioni si possono utilizzare queste due relazioni.
Esempio: data l'equazione
x2-3x-4=0 ha due soluzioni la cui somma vale -b/a=3/1=3 ed il cui prodotto vale c/a=-4/1=-4,
di conseguenza i due numeri sono 4 e -1 perchè la loro somma vale 3 ed il cui prodotto vale -4
Data l'equazione Ax2+Bx+c=0
Poiché il termine di secondo grado deve essere presente A non può annullarsi, quindi possono presentarsi i seguenti casi:
EQUAZIONE MONOMIA
L'equazione ha la forma Ax2=0, pertanto x2=0/A cioè x=0, di conseguenza un'equazione monomia ha una radice nulla
EQUAZIONE SPURIA
L'equazione ha la forma Ax2+Bx=0, posto x in evidenza si ottiene x(Ax+B)=0 essendo un prodotto uguale a zero allora, per la legge di annullamento del prodotto, almeno uno dei due fattori è zero,cioè si ha
x=0 o Ax+B=0 .
Si è ricondotta l'equazione di secondo grado alla risoluzione di due equazioni di primo, di cui una ha soluzione nulla.
L'altra soluzione è 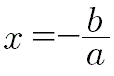
In questo abbiamo una equazione con due soluzioni sicuramente distinte di cui una è lo zero.
EQUAZIONE PURA
L'equazione ha la forma Ax2+C=0 che si può scrivere nella forma Ax2=-C, pertanto
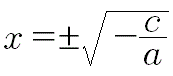
Il primo membro è sicuramente non negativo poiché è un quadrato allora deve esserlo anche il secondo membro. Se A e C sono concordi il secondo membro è negativo in quanto la frazione è preceduta dal segno meno, di conseguenza non si hanno radici, reali essendo il primo membro positivo. Se invece A e C sono discordi si hanno due radici reali opposte che si ottengono
{
Si supponga di dover trovare quel numero il cui quadrato sommato al suo doppio sia uguale a 63.
Indicato con x il numero cercato, il problema ci conduce a trovare la radice dell'equazione x2+2x=63
Poiché l'incognita compare con esponente massimo uguale a 2, si tratta di risolvere un'equazione di secondo grado.
Applicando le proprietà delle {tooltip class="tooltips tooltips-effect-4"}equazioni{end-link}uguaglianze fra due espressioni in cui compare una lettera detta incognita, sono verificate per particolari valori della stessa{end-tooltip}è sempre possibile ricondurre un'equazione di secondo grado nella cosìdetta forma normale
Ax2+Bx+C=0