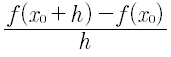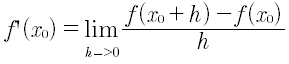Costante
funzione costante y=c y'=0
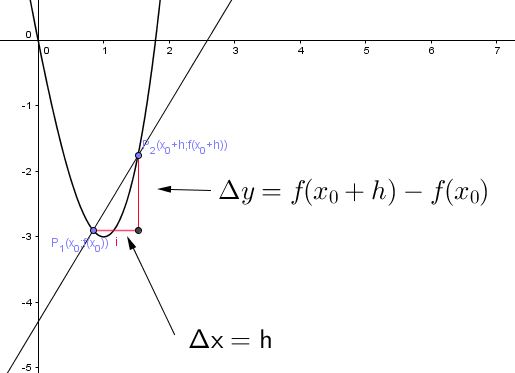
f(x0+h)=c, f(x0)=c pertanto il rapporto incrementale è sempre zero Si può spiegare questo risultat utilizzando la proprietà geometica di derivata in un punto. Infatti il coefficiente angolare di una retta è la derivata in tutti i suoi punti, in questo caso vale zero
Potenza
y=xn y'=xn-1
per n naturale si dimostra per induzione
infatti è vero per n=0 in quanto y=1 e y'=0
se è valida per un certo n, cioè se y=xn e y'=nxn-1
allora per y=xn+1 occorre dimostrare che y'=(n+1)•xn
y=xn+1 puo essere derivato con la regola del prodotto cioè y=xn•x
per cui y'=nxn-1•x +xn•1=nxn +xn=(n+1)•xn
Si puo far vedere che se n è reale vale la stessa formula
Seno
Si parte dalla definizione di derivata in x0
si utilizzano le regole di prostaferesi
.gif)
.gif)
ma .gif) e
e .gif)
pertanto il limite e di conseguenza la derivata vale cos(x0)
Coseno
Si parte dalla definizione di derivata in x0
si utilizzano le regole di prostaferesi
.gif)
.gif)
ex
.gif)
Arco tangente
Il tuo testo...




.gif)
.gif)
.gif)
.gif)
.gif) e
e .gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)