Il piano cartesiano
Un sistema di riferimento in un piano è costituito da due rette perpendicolari che chiamiamo asse x (o asse delle ascisse) e asse y (o asse delle ordinate).Il loro punto di intersezione è detto origine O degli assi cartesiani.
Sull'asse x si prende un punto U a cui si attribuisce l'ascissa 1. 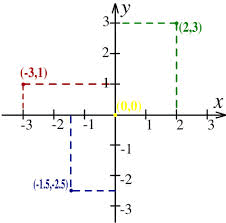 Pertanto ad ogni punto dell'asse x resta così associato un'ascissa, cioè un numero.
Pertanto ad ogni punto dell'asse x resta così associato un'ascissa, cioè un numero.
Allo stesso modo si procede per l'asse y.
In questo modo è possibile associare ad ogni punto del piano una coppia di numeri (x;y) che prendono il nome di coordinate del punto.
La prima coordinata prende il nome di ascissa, la seconda il nome di ordinata.
Gli assi cartesianio suddividono il piano in quattro quadranti numerati secondo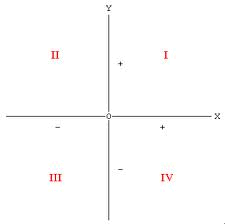 lo schema della figura.
lo schema della figura.
I segni delle cordinate dei punti nei singoli quadranti sono:
nel I (+;+);
nel II (-;+);
nel III (-;-);
nel IV (-;+).
Tutti i punti dell'asse x hanno ordinata uguale a zero, mentre tutti i punti dell'asse y hanno ascissa uguale a zero.
Le rette parallele all'asse x hanno la stessa ordinata, mentre le rette parallele all'asse y hanno la stessa ascissa.
Video sul piano cartesiano




 Pertanto ad ogni punto dell'asse x resta così associato un'ascissa, cioè un numero.
Pertanto ad ogni punto dell'asse x resta così associato un'ascissa, cioè un numero.  lo schema della figura.
lo schema della figura.