Definizione di limite
Limite finito per x che tende ad finito
Definizione.
Diciamo che il limite di f(x) per x che tende ad x0 vale l, in simboli
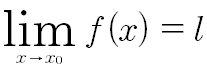
se comunque si prende ε>0 esiste un I(x0) completo del punto di accumulazione x0 in modo tale che per ogni x di I(x0) escluso al più il punto x0 si ha:
o in maniera equivalente
Osservazione la relazione l- ε< f(x)< l+ ε rappresenta due disuguaglianze
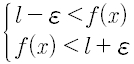
Esempio: verifichiamo che
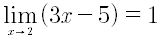
dobbiamo quindi trovare un intorno completo di 2 in modo tale che per ogni x appartenente a tale intorno si verifica
1-ε< 3x-5< 1+ε
si deve risolvere il sistema formato dalle due disequazioni
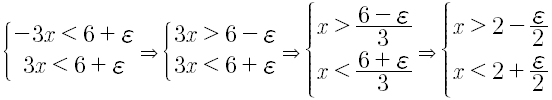
verificare che fra le soluzioni di tale sistema vi sia un intorno completo di 2
infatti le soluzioni sono
Definizione con Geogebra
Limite infinito per x che tende ad infinito
Definizione.
Diciamo che il limite di f(x) per x che tende a +∞ vale +∞, in simboli
se comunque si prende un K >0, esiste un'intorno I(+∞) di +∞ , cioè x>M>0, , si ha:
f(x)>K per ogni x>M.
In altre parole la f(x) tende ad l per x tendente ad ∞, quando scelto un qualunque intorno di l si trova un numero reale M
tale che per ogni x>M l'immagine cade nell'intorno scelto di l.
Limite finito per x che tende ad infinito
Definizione.
Diciamo che il limite è finito per x che tende ad infinito, l in simboli
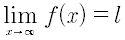
se comunque si prende ε>0 esiste un I(∞) completo di infinito cioè un intervallo della forma x>M , in modo tale che per ogni xєI(∞) si ha:
| f(x)-l |<ε
o in maniera equivalente
l-ε< f(x)< l+ε
In altre parole la f(x) tende ad l per x tendente ad ∞, quando scelto un qualunque intorno di l si trova un numero reale M tale che per ogni |x|>M l'immagine cade nell'intorno scelto di l.
Analoghe definizioni valgono per x->-∞, in tal caso per ogni x<-M deve aversi
| f(x)-l |<ε
Definizione con Geogebra
Limite infinito per x che tende ad finito
Definizione: diciamo che il limite di f(x) per x che tende ad x0 vale +∞,
in simboli

se comunque si prende un intorno di +∞, cioè un intervallo del tipo y >M esiste un'intorno I(x0) completo di x0, in modo tale che per ogni xє I(x0), escluso al più x0, si ha: f(x)>M.
In altre parole qualunque intorno di +∞ ha come controimmagini un insieme che contiene un intorno completo di x0, escluso al più x0 stesso.
Video sui limiti
Introduzione sui limiti
Limite per x tendente ad infinito
Limiti di funzioni razionali